常用算法

了解算法的概念，重点掌握排序相关算法。

算法概述

算法定义

算法是问题的可行的求解方法、规则和步骤。

算法有一下特征：

  • 有穷性

一个算法必须在执行有穷步骤之后结束；

  • 确定性

算法的每一步必须是确定的，不能有歧义；

  • 可行性

算法应该是可行的；

  • 输入

一个算个有零个或多个输入；

  • 输出

一个算个有零个或多个输出，他们是与输入有特定关系的量；

➡️ 一个算法的优劣可以从一下几个方面考虑：

  • 正确性
  • 可读性
  • 健壮性
  • 效率

算法与数据结构

算法实现总是建立在一定的数据结构基础之上。

数据结构 + 算法 = 程序。

算法的描述

常用的算法描述方法有流程图、N/S盒图、伪代码和决策表等。

P103页

算法效率

每个算法在计算机上执行时，都要消耗时间（CPU执行指令的时间）和使用存储空间资源。

算法运行时，所花费的时间和使用的空间，以时间复杂度和空间复杂度表示。

⭐ 重点：大O 表示法

算法往往和需要解决问题的规模相关，可以将问题规模n作为一个参照量。

对于一个算法的时间开销T(n), 从数量级大小考虑，当n增大一定值后，T(n)公式计算中影响最大的就是n的幂次最高项，其他的常数和低幂次项都可以忽略不计，即采用渐进分析，表示为 T(n)=O(f(n)) , 其中n反映问题的规模，T(n) 是算法运行时所消耗的时间或存储空间的总量，即常用的 大O表示法。

若 f(n) = n2 + 2 n + 1, 则 T(n) = O(n2).

提示

时间复杂度 O(1), O(n), O(n^2^) 分别称为常量阶、线性阶、和平方阶。

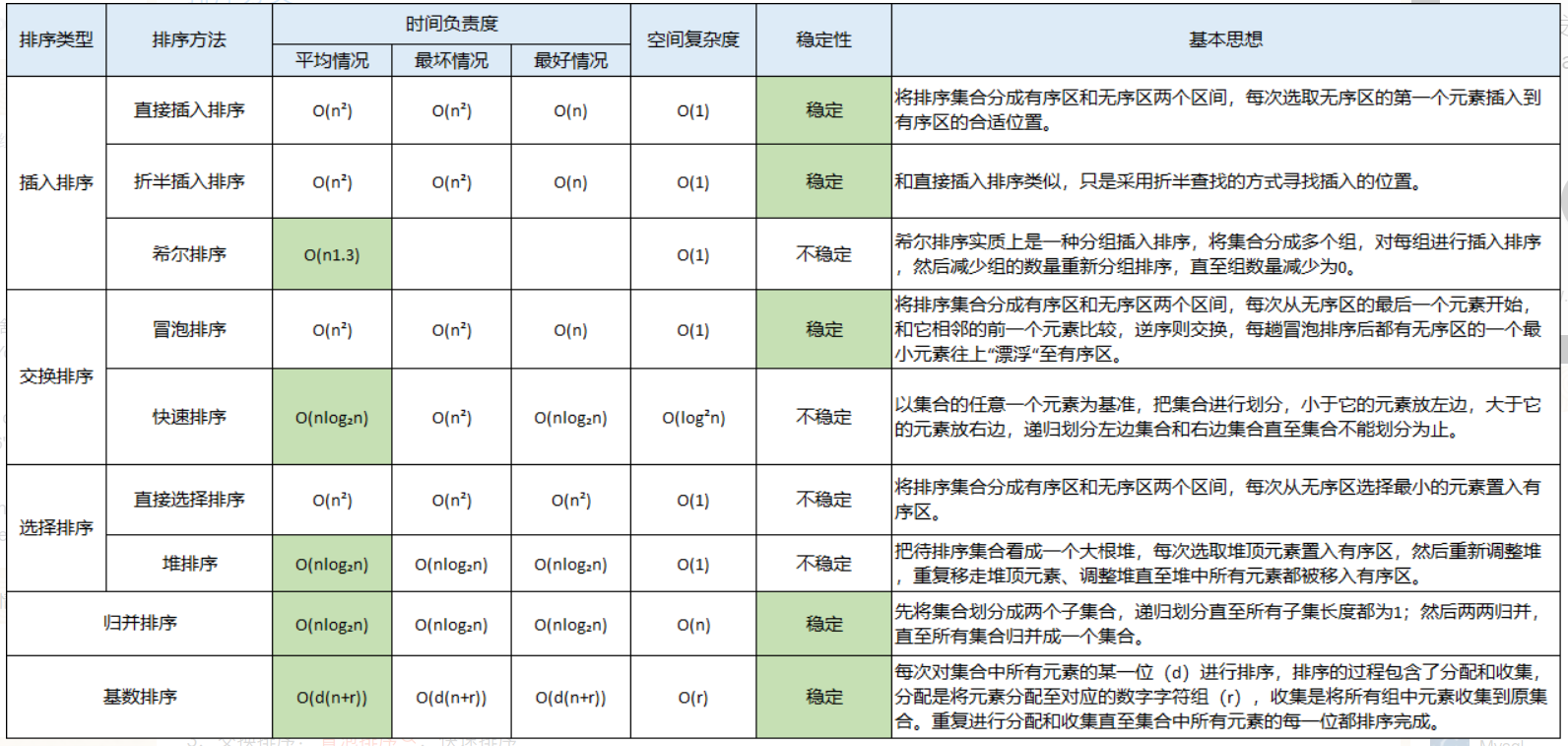
排序

参考：

排序算法 - 随笔分类 - Yadielr - 博客园 (cnblogs.com)

💯 什么是排序的稳定性？

① 定义：能保证两个相等的数，经过排序之后，其在序列的前后位置顺序不变。（A1=A2，排序前A1在A2前面，排序后A1还在A2前面）

② 意义：稳定性本质是维持具有相同属性的数据的插入顺序，如果后面需要使用该插入顺序排序，则稳定性排序可以避免这次排序。

比如，公司想根据“能力”和“资历”（以进入公司先后顺序为标准）作为本次提拔的参考，假设A和B能力相当，如果是稳定性排序，则第一次根据“能力”排序之后，就不需要第二次根据“资历”排序了，因为“资历”排序就是员工插入员工表的顺序。

如果是不稳定排序，则需要第二次排序，会增加系统开销。

☀️ 按稳定性排序的分类：

  • 稳定性排序：冒泡排序，插入排序、归并排序、基数排序
  • 不稳定性排序：选择排序、快速排序、希尔排序、堆排序

⚡ 内部排序和外部排序

  • 内部排序：待排序记录全部存放在内存中进行排序的过程。
  • 外部排序：待排序的数量巨大，以至于内存中不能容纳全部记录，在排序过程中，还需对外存进行访问。
image-20220405181650296

图片来源：九种常用排序算法_oceanao的博客-CSDN博客_常见排序算法

1️⃣ 简单插入排序

教材定义P106略。

算法简介 直接插入排序(Straight Insertion Sort)，把n个待排序的元素看成为一个有序表和一个无序表。开始时有序表中只包含1个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程。

算法描述

  • 1.从第一个元素开始，该元素可以被认为已经被排序
  • 2.取出下一个元素(i=1)，在已经排好序的序列中从后往前扫描
  • 3.直到找到小于或者等于该元素的位置
  • 4.将该位置后面的所有已排序的元素从后往前依次移一位
  • 5.将该元素插入到该位置
  • 6.重复步骤2~5

代码实现

function AnothorInsertion(arr) {
  var len = arr.length;
  for (var i = 1; i < len; i++) {
    //最核心的是：需要排位的元素先额外缓存起来
    var current = arr[i];
    var j = i - 1; //默认已排序的元素Index
    while (j >= 0 && arr[j] > current) {
      //在已排序好的队列中从后向前扫描
      arr[j + 1] = arr[j]; //已排序的元素大于新元素，将该元素移到一下个位置
      j--;
    }
    arr[j + 1] = current;
    console.log(arr.join(" ") + "\n");
  }
  return arr;
}
// 测试
var arr = [10, 8, 4, 2, 6];
//Insertion(arr);
AnothorInsertion(arr);

时间复杂度最好为o(n) 最坏为(n^2) ，平均为o(n2)

空间复杂度为o(1)

插入排序是一种稳定的排序方法。

2️⃣ 冒泡排序

冒泡排序(Bubble Sort)，每次遍历时，它都会从左往右依次地比较相邻两个数的大小，如果前者比后者大，则交换它们的位置。

一次遍历之后，将最大元素置于序列末尾。（或者从右往左每一次都将最小元素置于序列头部）

算法描述

  • 1.第一个n=0记录的关键字和第二个 n+1 记录的关键字进行比较
  • 2.若为逆序，则交换连个记录的值，即从小到大
  • 3.然后比较第2个记录个第三个寄了的关键字，重复步骤2
  • 4.以此内推，直到第n-1个记录和第n个记录的关键字比较完为止。
  • 5.以上完善第一轮排序。结果是最大的记录交换到第n个位置，即末尾。
  • 6.进行第二轮排序，对前n-1个记录进行同样的操作，完成第二轮排序后，次大的记录被交换到第n-1个位置。
  • 当进行到n-1趟时，所有记录有序排列。

代码实现：

var arr = [10, 8, 4, 2, 6];
console.log(arr.join(" ") + "\n");
function BubbleSort(arr) {
  let len = arr.length;
  for (var i = 0; i < len - 1; i++) {
    for (var j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        // 相邻元素两两对比
        //let temp = arr[j + 1]; // 元素交换
        //arr[j + 1] = arr[j];
        //arr[j] = temp;
        [arr[j],arr[j+1]] = [arr[j+1],arr[j]]
      }
    }
    //打印排序
    console.log(arr.join(" ") + "\n");
  }
  return arr;
}
BubbleSort(arr);

时间复杂度为o(n2)

空间复杂度为o(1)

插入排序是一种稳定的排序方法。

3️⃣ 简单选择排序

n个记录进行简单选择排序的节本方法是：通过n-i次关键字的比较，从n-i+1个记录中选出关键字最小的记录，并和第i （ 1<=i <=n )个记录进行交换。

当i = n 时，所有记录有序排列。

⚡ 基本思想是，首先在未排序的数列中找到最小(or最大)元素，然后将其存放到数列的起始位置；

接着，再从剩余未排序的元素中继续寻找最小(or最大)元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

代码实现：

console.log("-------简单选择排序demo---------");
var arr = [10, 8, 4, 2, 6];
console.log(arr.join(" ") + "\n");
function SortHandle(arr) {
  let len = arr.length;
  let minIndex = 0; // 假设第一个元素最小
  for (var i = 0; i < len; i++) {
    // 找出 i+1 -> len 之间的最小元素
    for (var j = i + 1; j < len; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }
    if (minIndex != i) {
      let temp = arr[i]; // 元素交换
      arr[i] = arr[minIndex];
      arr[minIndex] = temp;
    }
    //打印排序
    console.log(arr.join(" ") + "\n");
  }
  return arr;
}
SortHandle(arr);

时间复杂度为o(n2)

空间复杂度为o(1)

插入排序是一种不稳定的排序方法。

4️⃣ 希尔排序 Shell Sort

希尔排序又称“缩小增量排序”， 是对直接插入排序方法的改进。

特点是，在不断缩小增量的过程中，不断地排序，使得在最终使用插入排序时，序列已经基本有序。

插入排序在操作基本有序的序列时效率倍增。

希尔排序是不稳定的排序。

image-20220409211735903

图片来源：(55条消息) 排序 —— 希尔排序_一个很懒的人的博客-CSDN博客_希尔排序序列

Donald Shell最初建议步长选择为n/2并且对步长取半直到步长达到1。

虽然这样取可以比O(n^2)类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。

代码实现：

console.log("-------希尔排序demo---------");
var arr = [10, 8, 4, 2, 6];
console.log(arr.join(" ") + "\n");
function SortHandle(arr) {
  let len = arr.length;
  let gap = len / 2 | 0
  while (gap >= 1) {
    for (let outer = gap; outer < len; outer++) {
      const temp = arr[outer]
      let inner = outer
      while (inner - gap >= 0 && arr[inner - gap] > temp) {
        arr[inner] = arr[inner - gap]
        inner -= gap
      }
      arr[inner] = temp
    }
    gap = gap / 2 | 0
    //打印排序
    console.log(arr.join(" ") + "\n");
  }
  return arr;
}
SortHandle(arr);

5️⃣ 快速排序

快速排序的基本思想是：通过一趟排序将待排序的记录划分为独立的两部分，称为前半区和后半区。

其中，前半区中记录的关键字均不大于后半区记录的关键字，然后再分别对这两部分记录继续进行快速排序，从而使整个序列有序。

快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），简称快排，一种排序算法，最早由东尼·霍尔提出。

在平均状况下，排序n个项目要O($n\log_2{n}$)次比较。

在最坏状况下则需要O(n2)次比较，但这种状况并不常见。

事实上，快速排序通常明显比其他算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地达成

参看：js算法-快速排序(Quicksort) - SegmentFault 思否

🐱 快速排序的3个基本步骤：

  • 从数组中选择一个元素作为基准点
  • 排序数组，所有比基准值小的元素摆放在左边，而大于基准值的摆放在右边。每次分割结束以后基准值会插入到中间去。
  • 最后利用递归，将摆放在左边的数组和右边的数组在进行一次上述的1和2操作。

代码实现1：

//阮一峰版本
var quickSort = function (arr) {
    if (arr.length <= 1) {
        return arr;
    }
    var pivotIndex = Math.floor(arr.length / 2);
    //在js中splice会对数组进行一次拷贝的操作，而它最坏的情况下复杂度为O(n)，而O(n)代表着针对数组规模的大小进行了一次循环操作。
    var pivot = arr.splice(pivotIndex, 1)[0];
    var left = [];
    var right = [];
    for (var i = 0; i < arr.length; i++) {
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }
    return quickSort(left).concat([pivot], quickSort(right));
};

代码实现2：

var quickSort=function(arr,left,right){
  // 如果左边界比右边界大，返回结果，排序结束
  if(left>right){
    return;
  }
  // 默认值处理，如果有传入left和right参数，就赋值这个参数，否则就赋值后面的默认值
  left=left||0;
  right=right||arr.length-1;
  // 定义移动的左游标和右游标
  var leftPoint=left;
  var rightPoint=right;
  // 定义一个基准数
  var temp=arr[left];
  // 判断左右游标是否重合，如果重合，循环结束
  while(leftPoint!=rightPoint){
    // 基准数在左边，因此从右边开始一个个扫描
    // 从右到左，寻找小于基准数的数，且左游标要小于右游标
    // 如果数字大于基准数（证明不符合条件），寻找下一个
    // 直到找到比基准数小的数，游标停止递减
    while(arr[rightPoint]>=temp&&leftPoint<rightPoint){
      rightPoint--;
    }
    // 从左到右，寻找大于基准数的数，且左游标要小于右游标
    // 如果数字小于基准数（证明不符合条件），寻找下一个
    // 直到找到比基准数小的数，游标停止递增
    while(arr[leftPoint]<=temp&&leftPoint<rightPoint){
      leftPoint++;
    }
    // 如果左游标小于右游标，则交换两个数字的位置
    if(leftPoint<rightPoint){
      var changeNumber=arr[leftPoint];
      arr[leftPoint]=arr[rightPoint];
      arr[rightPoint]=changeNumber;
    }
    // 进行下一次循环，直到两个游标重合位置
  }
  // 重合之后，交换基准数
  arr[left]=arr[leftPoint];
  arr[leftPoint]=temp;
  // 递归操作左右两个数组
  quickSort(arr,left,leftPoint-1);
  quickSort(arr,leftPoint+1,right);
  return arr;
};
var numArr=[6,1,2,7,9,4,5,10,8];
console.log(quickSort(numArr));

6️⃣ 堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(n$\log_2{n}$)，

它也是不稳定排序。

首先简单了解下堆结构。

堆

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

image-20220410110234777

堆排序的基本思想是：

将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

7️⃣ 归并排序

归并排序，是创建在归并操作上的一种有效的排序算法。

算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

归并排序思路简单，速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。

归并排序是用分治思想，分治模式在每一层递归上有三个步骤：

  • 分解（Divide）：将n个元素分成个含n/2个元素的子序列。
  • 解决（Conquer）：用合并排序法对两个子序列递归的排序。
  • 合并（Combine）：合并两个已排序的子序列已得到排序结果。

平均时间复杂度：O($n\log_2{n}$) 最佳时间复杂度：O(n) 最差时间复杂度：O($n\log_2{n}$) 空间复杂度：O(n) 排序方式：In-place 稳定性：稳定

8️⃣ 折半插入排序（二分插入）

⭐ 大纲无要求

9️⃣ 基数排序

⭐ 大纲无要求

查找

递归

图的相关算法