数据库设计理论基础
# 参考:https://www.zhihu.com/question/24696366
# 如何理解关系型数据库的常见设计范式?⚡ 💯 范式的每年必考的重点知识
关系数据库设计理论的核心是数据之间的函数依赖,衡量的标准是关系规范化的程度以及分解的无损连接和保持函数依赖性。
数据依赖是通过一个关系中属性间值的相等与否体现出来的数据间的相互关系。是现实世界属性间联系和约束的抽象,是数据内在的性质,是语义的体现。
函数依赖是一种最重要的、最基本的数据依赖。
⚡ 讨论数据依赖,一定是讨论关系模式中属性间的逻辑依赖关系。 属性!属性!属性!
函数依赖
💯 必须掌握完全函数依赖、部分函数依赖、传递函数依赖的概念。
学生关系:S(Sno,Sname,Sage,Dept);
| 学生编号Sno | 学生姓名Sname | 学生年龄Sage | 所在系Dept |
|---|---|---|---|
| 001 | 张三 | 20 | 计算机 |
由于一个学生编号对应一个学生,而一个学生只属于一个系。
所以当学生编号确定之后,学生姓名、年龄、所在系的值也唯一确定了。
即 : Sno 决定函数(Sname,Sage,Dept), 或者是 函数(Sname,Sage,Dept)依赖于Sno 。
表示为:Sno->(Sname,Sage,Dept);
抽象成:X->Y(Y依赖于X,X决定Y)。
⚡ 非平凡函数依赖与平凡函数依赖
非平凡函数依赖和平凡函数依赖的区别就在于X包不包含Y,也就是Y是不是X的子集的区别。
比如:非平凡:Sno->(Sname,Sage,Dept), 不包含,即非平凡函数依赖。一般情况下总是讨论非平凡函数依赖。
如果同时还存在一个 选课关系:SC(Sno,Cno,score)
| 学生编号Sno | 课程编号Cno | 学分score |
|---|---|---|
| 001 | c01 | 20 |
(Sno,Cno)->Cno ,且Cno 是(Sno,Cno)的子集,则为平凡函数依赖。
If a functional dependency X->Y holds true where Y is not a subset of X then this dependency is called non trivial Functional dependency.
🌹 trivial: 平凡的,不重要的。如果 y 是 x 的子集,且 x-y, 例如 {emp_id, emp_name} -> emp_name, 则讨论起来完全没有意义,即平凡函数依赖。
⚡ 完全函数依赖与局部函数依赖
在关系模式R(U)中,U是属性全集,X和Y是U的子集,如果X->Y,并且对于X的任何一个真子集X',都有X'不决定Y,则称Y对X完全函数依赖。
否则称为部分函数依赖,也称局部函数依赖。
⚠️ 注意:只有当决定因素是组合属性的时候,讨论部分依赖才有意义,当决定因素是单属性的时候,只能是完全函数依赖。
例如,Sno->(Sname,Sage,Dept), 决定因素是Sno,不存在部分函数依赖
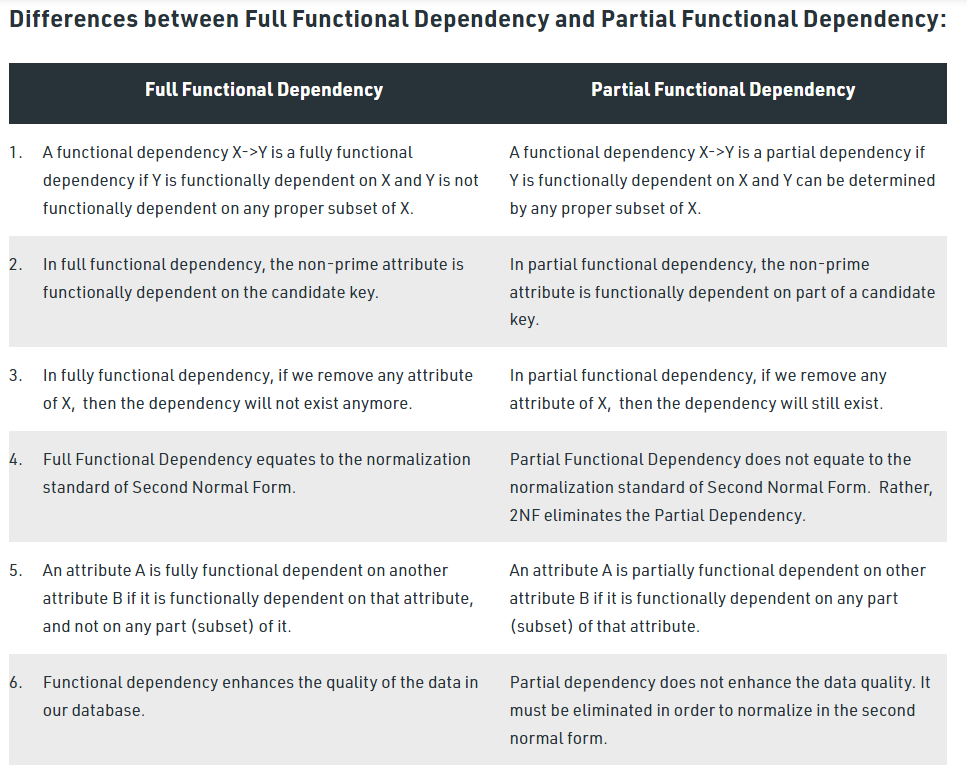
如果要满足第2范式,必须消除部分函数依赖。
图片来源:
Differentiate between Partial Dependency and Fully Functional Dependency - GeeksforGeeks
⚡ 传递函数依赖与直接函数依赖
设关系模式R(U), U是属性全集,X和Y是U的子集,X,Y,Z是U的子集。若X->Y,Y->Z, 但Y不决定X,则称Z对X传递函数依赖。
但是如果X<->Y,则称Z对X直接函数依赖。
比如:学号->班级,班级->讲师,但是讲师不能决定班级,所以讲师对学号是传递函数依赖。
假设学生不重名,学号决定学生名,学生名决定学号,学生名决定了班级,这时候班级对学号是直接函数依赖。
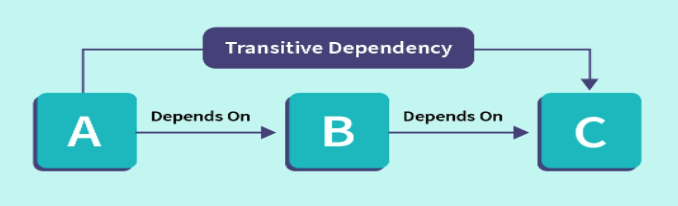
A transitive dependency in a database is an indirect relationship between values in the same table that causes a functional dependency. To achieve the normalization standard of Third Normal Form (3NF), you must eliminate any transitive dependency.
即:要满足第三范式,必须消除传递函数依赖。
参考:
码和属性
💯 需要掌握超码、候选码、主码、主属性、非主属性等概念。
候选码/候选关键字
设 K 为某表R(U、F)中的一个属性或属性组,若除 K 之外的所有属性都完全函数依赖于 K(这个“完全”不要漏了),那么我们称 K 为候选码
简言之,如果关系中的某一属性组的值能唯一地标识一个元组,则称该属性组为候选码。
即 K-->U,且K的任何一个真子集不能决定U(教材定义)
主码/主键
如果一个关系有多个候选码,则选定其中一个为主码;
主属性
包含在任何一个候选码中的属性,即为主属性。
非主属性
不包含在任何一个候选码中的属性,即为主属性。
多值依赖
P281,略
规范化(范式)
关系数据库设计的方法之一就是设计满足适当范式的模式,可以通过判断分解后的模式达到几范式来评价模式规范化的程度。
通过分解,可以将一个第一级范式的关系模式转换成若干个高一级范式的关系模式,这种过程叫作规范化。
1️⃣ 1NF
教材概念:关系模式R的每一个分量是不可再分的数据项。
简言之:关系中的每个属性都不可再分。
2️⃣ 2NF
教材概念:关系模式R属于1NF,且每一个非主属性完全依赖于码。
简言之:1NF的基础之上,消除了非主属性对于码的部分函数依赖。
3️⃣ 3NF
教材概念:略
简言之:在2NF的基础之上,消除了非主属性对于码的传递函数依赖。
4️⃣BCNF
教材概念: 略
简言之:在3NF的基础之上,消除主属性对于码的部分与传递函数依赖。
Armstrong 公理系统
⭐ 主要考点
Armstrong 公理系统
在充分条件假言判断中:**如果P,那么Q,可以表示为P→Q**
P称为前件(条件),Q称为后件(后果),“→”这个符号,逻辑叫做“蕴涵”
Armstrong公理系统,也称函数依赖的公理系统。
设关系模式R(U,F),其中U为属性集,F是U上的一组函数依赖,那么有如下推理公式:

包含:对于两个集合A,B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集。
记作: A⊆B(或B⊇A) 读作:“A包含于B”(“B包含A”)。此时,A就是属于B。
真包含的言外之意就是真子集。
如果集合A⊆B,但存在元素X∈B,且元素X不属于集合A,我们称集合A是集合B的真子集。
也就是说如果集合A的所有元素同时都是集合B的元素,则称A是B的子集, 若B中有一个元素,而A 中没有,且A是B的子集,则称A 是B的真子集。
⭐ 重点掌握 增广率 和 伪传递率。

函数依赖的闭包F+ 及属性闭包X+F
见补充章节
闭包就是由一个属性直接或间接推导出的所有属性的集合。
例如:f= {a->b,b->c,a->d,e->f };
由a可直接得到b和d,间接得到c,则a的闭包就是{ a,b,c,d }
候选码的求解
见补充章节
最小函数依赖集
见补充章节
⚡ 相关真题
2014年33-35题
给定关系模式R(U,F),U={A,B,C,D},函数依赖集F={AB→C,CD→B}。关系模式R(33),且分别有(34)。
若将R分解成p={R1(ABC),R2(CDB)},则分解p(35)。
(33) A.只有1个候选关键字ACB
B.只有1个候选关键字BCD
C.有2个候选关键字ACD和ABD
D.有2个候选关键字ACB和BCD
(34) A.0个非主属性和4个主属性
B.1个非主属性和3个主属性
C.2个非主属性和2个主属性
D.3个非主属性和1个主属性
(35) A.具有无损连接性、保持函数依赖
B.具有无损连接性、不保持函数依赖
C.不具有无损连接性、保持函数依赖
D.不具有无损连接性、不保持函数依赖
【答案】C A C
【解析】本题考查关系数据库规范化理论方面的基础知识。
(33) 根据函数依赖定义,可知ACD→U, ABD→U,所以ACD和ABD均为候选关键字。
(34) 根据主属性的定义“包含在任何一个候选码中的属性叫做主属性(Prime attribute),否则叫做非主属性(Nonprime attribute)”,
所以,关系R中的4个属性都是主属性。
(35)根据无损连接性判定定理:
关系模式R分解为两个关系模式R1、R2,满足无损连接性的充分条件是R1∩R2→(R1---R2)或R1∩R2→(R2---R1), 能由函数依赖集F逻辑地推出。由于R1∩R2=BC,R1--R2=A,但BC→A不能由函数依赖集F逻辑地推出;同理,R2-R1=D,但BC→D不能由函数依赖集F逻辑地推出,故分解不满足无损连接性。
由保持函数依赖的定义,若满足(F1UF2)+=F+,则分解保持函数依赖,其中Fi函数依赖集F在Ri上的投影。由题目,(F1UF2) =F,即(F1UF2) +=F+ 成立,故分解保持函数依赖。
关于无损连接和函数依赖保存,待复习
判断模式分解是否具有无损链接性 - 光何 - 博客园 (cnblogs.com)
具体看B站视频吧
2014年57题
通过反复使用保证无损连接性,又保持函数依赖的分解,能保证分解之后的关系模式至少达到(57)。
A.1NF B.2NF C.3NF D.BCNF
【答案】C
关系模式的分解,必须保证分解具有无损连接性,即分解能够被还原,否则会发生信息丢失(通过自然连接还原关系时会产生多余的记录)。
分解保持函数依赖,至少能到 3NF。
2015年35/36题
给定关系模式R(A1,A2,A3,A4),R上的函数依赖集F= {A1A3→A2,A2→A3},R(35)。
A.有一个候选关键字A1A3
B.有一个候选关键字A1A2A3
C.有二个候选关键字A1A3A4和A1A2A4
D.有三个候选关键字A1A2,A1A3和A1A4
若将R分解为p={(A1,A2,A4),(A1,A3)}.那么该分解是(36)的。
A.无损联接
B.无损联接且保持函数依赖
C.保持函数依赖
D.有损联接且不保持函数依赖
【答案】C D
因为A1A3→A2,A2→A2,没有出现A4,所以候选关键字中肯定包含A4,
属性A1A3A4决定全属性,故为候选关键字。
同理A1A2A4也为候选关键字。
设U1={A1,A2,A4},U2={A1,A3},那么可得出:(U1∩U2)→(U1-U2)=A1→A2,(U1∩U2)→(U1-U2)=A1→A3,
而A1→A2,A1→A3∉F+所以分解ρ是有损连接的。
又因为F1=F2=∅,F+≠(F1∪F2)+,所以分解不保持函数依赖。